Interaction

class: center, middle, inverse, title-slide

# Interaction
## What If: Chapter 5
### Elena Dudukina
### 2020-12-08

---

# Definition of the interaction
* The joint intervention of two or more treatments
- A: heart transplant
- E: vitamins
- 4 treatment combinations: `\(Y^{a=0, e=0}, Y^{a=1, e=0}, Y^{a=0, e=1}, Y^{a=1, e=1}\)`
- Effect measured on the absolute scale: interaction on the additive scale `\(Pr[Y^{a=1, e=1}=1]-Pr[Y^{a=0, e=1}=1] \neq Pr[Y^{a=1, e=0}=1]-Pr[Y^{a=0, e=0}=1]\)`
- Example: 
    - the causal risk difference for receiving the transplant when everyone gets vitamins `\(Pr[Y^{a=1, e=1}=1]-Pr[Y^{a=0, e=1}=1]\)`=0.1 and the causal risk difference for receiving the transplant when no one gets vitamins `\(Pr[Y^{a=1, e=0}=1]-Pr[Y^{a=0, e=0}=1]\)`=0.2
    - 0.1 `\(\neq\)` 0.2
    - there is an interaction on the additive scale between treatments A and E
    - same implied for the second exposure E: `\(Pr[Y^{a=1, e=1}=1]-Pr[Y^{a=1, e=0}=1] \neq Pr[Y^{a=0, e=1}=1]-Pr[Y^{a=0, e=0}=1]\)`
    - both exposures have an equal status and require the same assumptions
    - in contrast to the effect measure modification, which deals with the causal effect of only one exposure and the causal contrast is defined in terms of the P.O. `\(Y^a\)`, interaction deals with **joint** effect of several exposures and the causal contrast defined  in terms of the P.O. `\(Y^{a, e}\)`
---
# Technical point 5.1
- Working with the interaction equation:
    * `\(Pr[Y^{a=1, e=1}=1]-Pr[Y^{a=1, e=0}=1] \neq Pr[Y^{a=0, e=1}=1]-Pr[Y^{a=0, e=0}=1]\)` -->
    * `\(Pr[Y^{a=1, e=1}=1] \neq {Pr[Y^{a=0, e=1}=1]-Pr[Y^{a=0, e=0}=1]}+Pr[Y^{a=1, e=0}=1]\)` -->
    * substruct `\(Pr[Y^{a=0, e=0}=1]\)`:
    * `\(Pr[Y^{a=1, e=1}=1] - Pr[Y^{a=0, e=0}=1] \neq \\{Pr[Y^{a=0, e=1}=1]-Pr[Y^{a=0, e=0}=1]}+Pr[Y^{a=1, e=0}=1] - Pr[Y^{a=0, e=0}=1]\)`
- Multiplicative scale:
    * `\(\frac{Pr[Y^{a=1, e=1}=1]}{Pr[Y^{a=0, e=0}=1]} \neq \frac{Pr[Y^{a=1, e=0}=1]}{Pr[Y^{a=0, e=0}=1]} * \frac{Pr[Y^{a=0, e=1}=1]}{Pr[Y^{a=0, e=0}=1]}\)`
---
# Identifying interaction
- Exchangeability, positivity, and consistency for both exposures
- Imagine E was assigned marginally (unconditionally) at random `\(Pr[Y^{a=1, e=1}=1]\)` under exchangeability becomes `\(Pr[Y^{a=1}=1|E=1]\)`
    * For the full equation: `\(Pr[Y^{a=1, e=1}=1]-Pr[Y^{a=0, e=1}=1] \neq Pr[Y^{a=1, e=0}=1]-Pr[Y^{a=0, e=0}=1]\)`
    * under exchangeability:
    * `\(Pr[Y^{a=1}=1|E=1]-Pr[Y^{a=0}=1|E=1] \neq Pr[Y^{a=1}=1|E=0]-Pr[Y^{a=0}=1|E=0]\)`
- When treatment E is randomly assigned, the interaction and effect modification coincide
---
- A and E are **joint** inrervention --> combined treatment AE with four possible levels (11, 01, 10, 00)
- Identification of the causal effect of one treatment AE
---

# Counterfactual response types

| Type | `\(Y^{a=0}\)`   | `\(Y^{a=1}\)`  |
|------:|:-----|---------|
|   Doomed  |  1  |    1   |
|  Helped  |  1 |   0   |
|    Hurt  |    0 |     1   |
|    Immune  |    0 |     0   |
---
**Counterfactual response types**

```
## # A tibble: 20 x 4
##    greek       Y_a0  Y_a1 type  
##    <chr>      <dbl> <dbl> <chr> 
##  1 Demeter        0     0 immune
##  2 Hades          0     0 immune
##  3 Hestia         0     0 immune
##  4 Hera           0     0 immune
##  5 Rheia          0     1 hurt  
##  6 Zeus           0     1 hurt  
##  7 Leto           0     1 hurt  
##  8 Hephaestus     0     1 hurt  
##  9 Aphrodite      0     1 hurt  
## 10 Cyclope        0     1 hurt  
## 11 Kronos         1     0 helped
## 12 Poseidon       1     0 helped
## 13 Apollo         1     0 helped
## 14 Hermes         1     0 helped
## 15 Hebe           1     0 helped
## 16 Dionysus       1     0 helped
## 17 Artemis        1     1 doomed
## 18 Ares           1     1 doomed
## 19 Athena         1     1 doomed
## 20 Persephone     1     1 doomed
```
---
**Counterfactual response types**

<table>
 <thead>
  <tr>
   <th style="text-align:right;"> type </th>
   <th style="text-align:right;"> Y_a=1, e=1 </th>
   <th style="text-align:right;"> Y_a=0, e=1 </th>
   <th style="text-align:right;"> Y_a=1, e=0 </th>
   <th style="text-align:right;"> Y_a=0, e=0 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 5 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 6 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 7 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 8 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 9 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 10 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 11 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 12 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 13 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 14 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 16 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
</tbody>
</table>
---
# Counterfactual response types

- Type 1 dies regardless of the treatments received
- Type 16 is immune
<table>
 <thead>
  <tr>
   <th style="text-align:right;"> type </th>
   <th style="text-align:right;"> Y_a=1, e=1 </th>
   <th style="text-align:right;"> Y_a=0, e=1 </th>
   <th style="text-align:right;"> Y_a=1, e=0 </th>
   <th style="text-align:right;"> Y_a=0, e=0 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 16 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
</tbody>
</table>
---
- Type 4 dies if treated with E regardless of A
- Type 13 dies if NOT treated with E regardless of A
- Type 6 dies if treated with A regardless of E
- Type 11 dies if NOT treated with A regardless of E

<table>
 <thead>
  <tr>
   <th style="text-align:right;"> type </th>
   <th style="text-align:right;"> Y_a=1, e=1 </th>
   <th style="text-align:right;"> Y_a=0, e=1 </th>
   <th style="text-align:right;"> Y_a=1, e=0 </th>
   <th style="text-align:right;"> Y_a=0, e=0 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 6 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 11 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 13 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
</tbody>
</table>
---
# Counterfactual response types
- The response types 1, 4, 6, 11, 1, 16: causal effect of A on Y is the same regardless of E and vice versa for the effect of E on Y regardless of A
- If all individuals in the population have these response types, there is no interaction between A and E
    - `\(Pr[Y^{a=1, e=1}=1] - Pr[Y^{a=0, e=1}=1] = Pr[Y^{a=1, e=0}=1] - Pr[Y^{a=0, e=0}=1]\)` 
- Interaction is present when there are individuals of:
* Types 8, 12, 14, 15 (outcome under only one of the four treatment combinations)
  
<table>
 <thead>
  <tr>
   <th style="text-align:right;"> type </th>
   <th style="text-align:right;"> Y_a=1, e=1 </th>
   <th style="text-align:right;"> Y_a=0, e=1 </th>
   <th style="text-align:right;"> Y_a=1, e=0 </th>
   <th style="text-align:right;"> Y_a=0, e=0 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 8 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 12 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 14 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
</tbody>
</table>

* Types 7 and 10
<table>
 <thead>
  <tr>
   <th style="text-align:right;"> type </th>
   <th style="text-align:right;"> Y_a=1, e=1 </th>
   <th style="text-align:right;"> Y_a=0, e=1 </th>
   <th style="text-align:right;"> Y_a=1, e=0 </th>
   <th style="text-align:right;"> Y_a=0, e=0 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 7 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 10 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
</tbody>
</table>
---
* Types 2, 3, 5, and 9 (outcome under 3 put of 4 combinations)
<table>
 <thead>
  <tr>
   <th style="text-align:right;"> type </th>
   <th style="text-align:right;"> Y_a=1, e=1 </th>
   <th style="text-align:right;"> Y_a=0, e=1 </th>
   <th style="text-align:right;"> Y_a=1, e=0 </th>
   <th style="text-align:right;"> Y_a=0, e=0 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 5 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 9 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
</tbody>
</table>
---
# Monotonicity
- The causal effects of A and E on Y are monotonic if every individual’s counterfactual outcomes `\(Y^{a, e}\)` are monotonically increasing in both a and e (technical point 5.2)
    - There are no types `\(Y^{a=1, e=1}=0, Y^{a=0, e=1}=1\)`, etc.
---
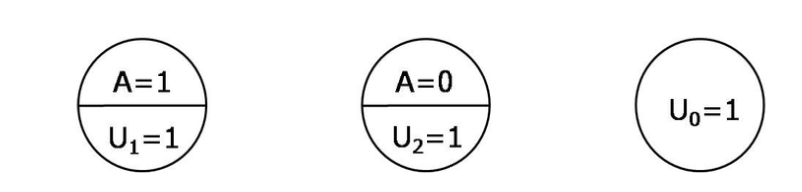
# Sufficient causes
- Different responses types indicate that treatment A alone is not enough to always cause the outcome Y
- Minimal sufficient causes are A=1 & U1=1 and A=0 & U2=1 and U0
- Each sufficient cause has components --> sufficient-component causes
![:scale 50%](Screenshot 2020-12-08 at 21.16.35.png)
---
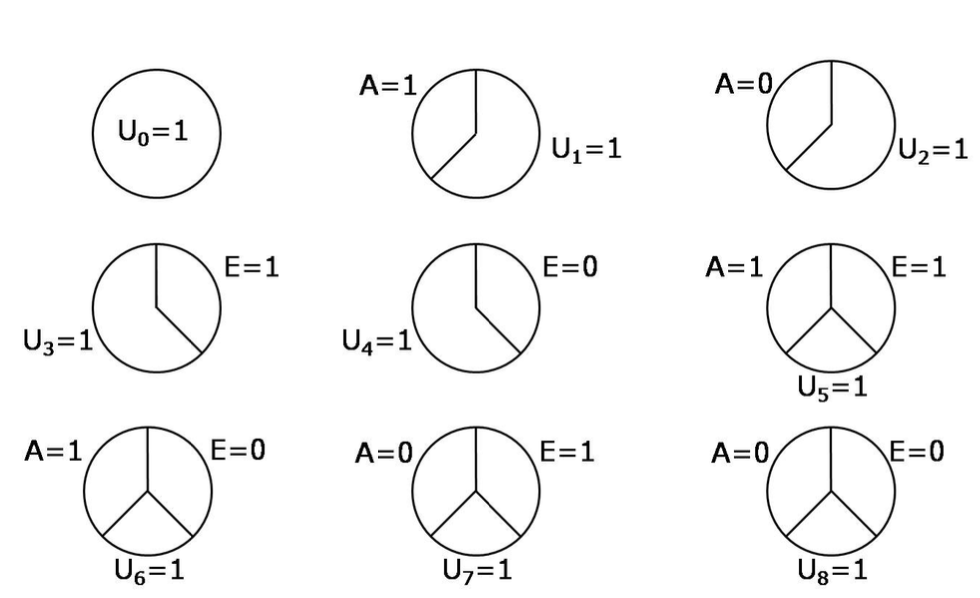
# Sufficient causes
- 9 possible sufficient causes with treatment components A = 1 only, A = 0 only, E = 1 only, E = 0 only, A = 1 and E = 1, A = 1 and E = 0, A = 0 and E = 1, A = 0 and E = 0, and neither A nor E matter.
![:scale 50%](Screenshot 2020-12-08 at 21.23.55.png)